近世代数
基本概念
集合、映射、变换
代数运算、运算律
同态与同构
等价关系与集合分类
群
群的定义与基本性质
循环群
变换群
置换群
陪集指数与Largrange定理
群同态基本定理与正规子群
性质
正规子群
- 证明:指数为2的子群必是正规子群
证明思路:
要证明一个子群 H 是正规子群,需要证明对于群 G 中任意元素 g,都有 gH=Hg。对于指数为2的子群,我们可以利用陪集的性质来证明。
证明过程:
设 G 是一个群,H 是 G 的一个子群,且 ∣G:H∣=2。
这意味着 H 在 G 中只有两个不同的左陪集和两个不同的右陪集。
其中一个左陪集是 H 本身(即 eH=H),另一个左陪集是 G 中不属于 H 的任意元素 a 所生成的 aH。
所以,G=H∪aH。
同样地,右陪集也有两个:一个右陪集是 H 本身(即 He=H),另一个右陪集是 a 所生成的 Ha。所以,G=H∪Ha。
现在我们来证明对于 G 中任意元素 g,都有 gH=Hg。
情况1: g∈H。
如果 g∈H,那么 gH=H 且 Hg=H。所以 gH=Hg 成立。
情况2: g∈/H。
如果 g∈/H,那么 g 属于 H 的另一个左陪集,即 gH。
由于 G=H∪aH,且左陪集要么相等要么不相交,所以 gH 必须等于 aH。
即 gH=aH。同样地,如果 g∈/H,那么 g 属于 H 的另一个右陪集,即 Hg。
由于 G=H∪Ha,所以 Hg 必须等于 Ha。
即 Hg=Ha。
现在我们来证明 aH 和 Ha 相等。
因为 G 由 H 和另一个陪集组成,所以 G∖H=aH=Ha。
所以 gH=aH=G∖H 和 Hg=Ha=G∖H。
因此,gH=Hg。
综上所述,对于 G 中任意元素 g,都有 gH=Hg。所以,指数为2的子群必是正规子群。
2. 证明:若群 G 的 n 阶子群只有一个,则此子群必为 G 的正规子群
证明思路:
这个证明需要利用共轭子群的概念。如果一个子群经过共轭运算后仍然是它自己,那么它就是正规子群。
证明过程:
设 G 是一个群,H 是 G 中唯一的 n 阶子群。
我们需要证明 H 是一个正规子群,即对于 G 中任意元素 g,都有 gHg−1=H。
首先,我们考虑由 H 通过共轭运算得到的集合 gHg−1={ghg−1∣h∈H}。
我们来证明这个集合 gHg−1 也是一个子群。
单位元:e=geg−1∈gHg−1,因为 e∈H。所以 gHg−1 包含单位元。
封闭性:对于任意两个元素 a=gh1g−1 和 b=gh2g−1,它们的乘积是 ab=(gh1g−1)(gh2g−1)=g(h1h2)g−1。因为 h1,h2∈H,所以 h1h2∈H。因此,ab∈gHg−1。
逆元:对于任意元素 a=ghg−1,其逆元是 a−1=(ghg−1)−1=(g−1)−1h−1g−1=gh−1g−1。因为 h−1∈H,所以 a−1∈gHg−1。所以,gHg−1 是群 G 的一个子群。
接下来,我们来计算它的阶数。
考虑映射 ϕ:H→gHg−1,定义为 ϕ(h)=ghg−1。
这个映射是一个同构:
- 它是单射:如果 ϕ(h1)=ϕ(h2),那么 gh1g−1=gh2g−1。左乘 g−1,右乘 g,得到 h1=h2。所以它是单射。
- 它是满射:对于 gHg−1 中任意元素 x,存在 h∈H 使得 x=ghg−1,所以它是满射。
因此,ϕ 是一个双射,所以 ∣gHg−1∣=∣H∣=n。
现在我们有两个重要的结论:
- gHg−1 是 G 的一个子群。
- gHg−1 的阶数为 n。
根据题设,群 G 中唯一的 n 阶子群是 H。
因此,这个新生成的 n 阶子群 gHg−1 必须就是 H 本身。
所以,gHg−1=H。
由于这个结论对于 G 中任意元素 g 都成立,所以 H 是一个正规子群。
所以,若群 G 的 n 阶子群只有一个,则此子群必为 G 的正规子群。

























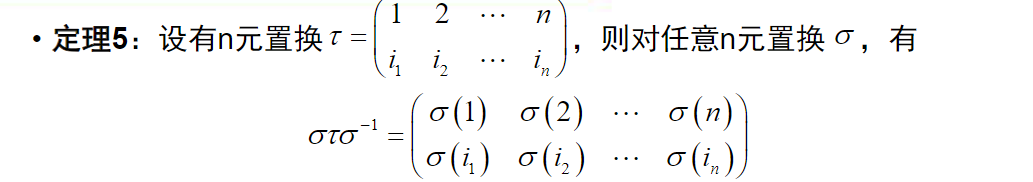
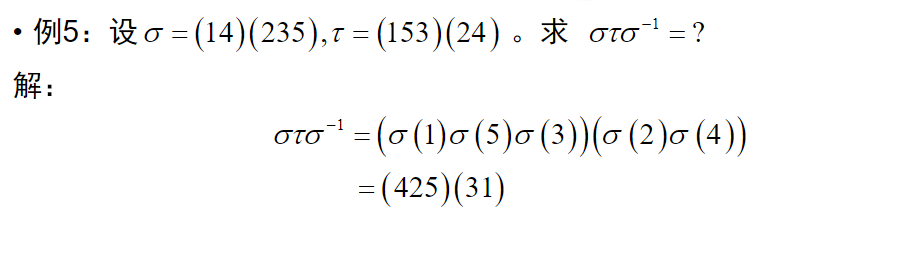


















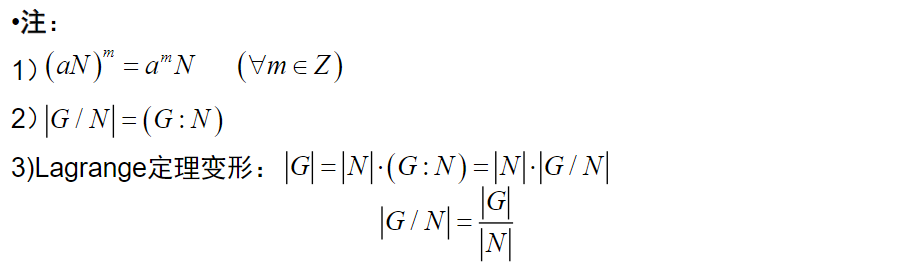
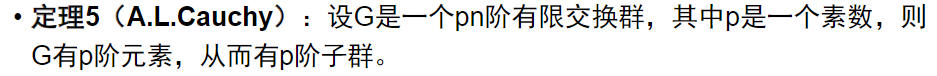



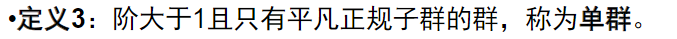








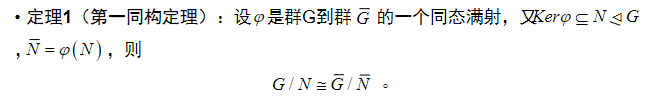

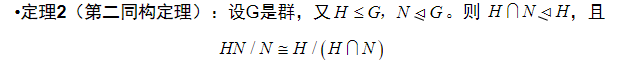

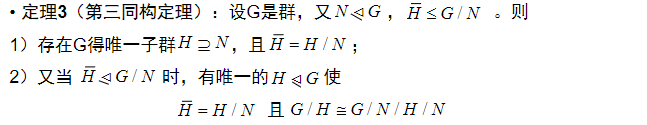















,(ultra%20highest%20quality),(ultra%20detailed),highres,ultimate%20beauty,high%20saturation,vivid,(cute%20girl),heart,-fmzp.png)